什么是红黑树?
红黑树(Red-Black-Tree)是在 1972 年由鲁道夫·贝尔发明,被称为”对称二叉 B 树”,是一种由红黑节点组成并能自平衡的二叉查找树
红黑树保证了最坏情形下在 O(log2N) 时间复杂度内完成查找、插入及删除操作;因此红黑树可用于很多场景,比如在 Java 的集合框架 (HashMap、TreeMap、TreeSet)、Nginx 的 Timer 管理、Linux 虚拟内存管理以及 C++ 的 STL 等等都能看到它的应用
- 为什么要红黑树?
二叉查找树并非平衡树,它只限制了左右子树与根点之间的大小关系,只有在平衡二叉查找树时,其时间复杂度才能达到 O(log2N) ,并且在极端情况下它甚至会退化成链表
红黑树的性质
每个节点或者是黑色或者是红色
根节点是黑色
每个叶子节点(null)是黑色
如果一个节点是红色,则它的子节点必须是黑色,即两个红色节点不能直接相连
从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑色节点
红黑树的五个性质避免了二叉查找树退化成单链表的情况,并且性质 4 和性质 5 确保了任意节点到其每个叶子节点路径中最长路径不会超过最短路径的 2 倍,即一颗树是黑红节点相间的树,另一颗全是黑节点的树;也就是红黑树是相对黑色节点的平衡二叉树
自平衡的实现
红黑树节点的插入和删除可能会破坏上述红黑树的性质并打破它的平衡,因此需要进行调整从而让红黑树重新恢复平衡;调整分两种方式:旋转以及变色
左旋(Rotate Left)
左旋的过程是将x的右子树绕x逆时针旋转,使得x的右子树成为x的父亲,同时修改相关节点的引用。旋转之后,二叉查找树的属性仍然满足
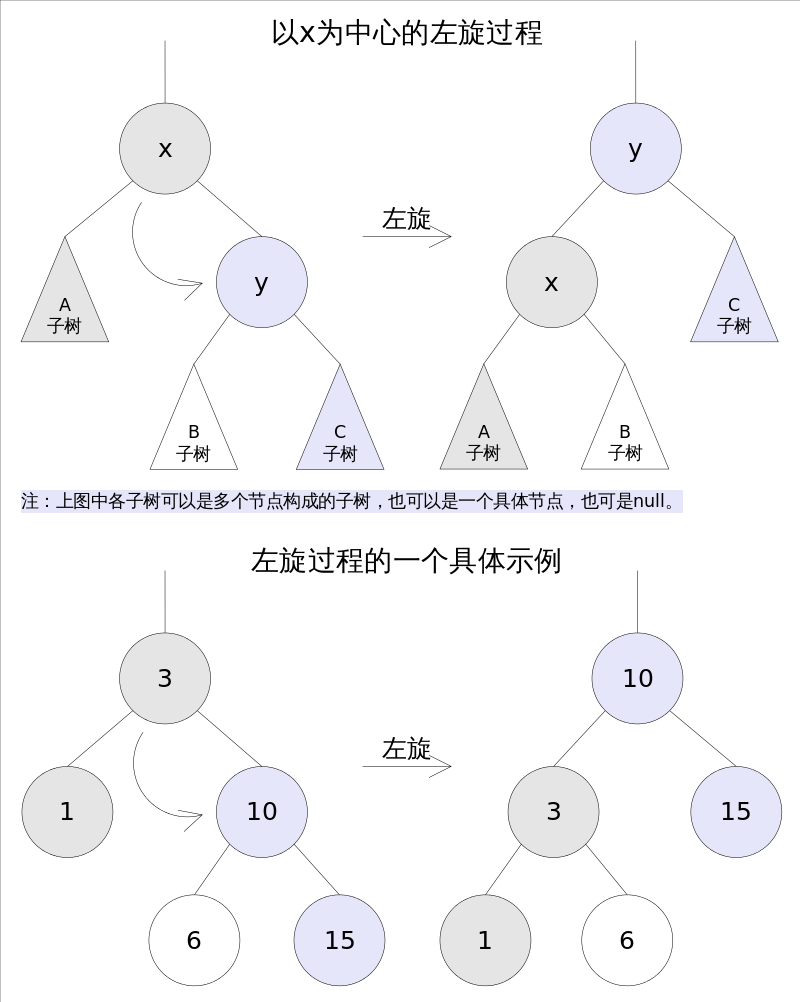
右旋(Rotate Right)
右旋的过程是将x的左子树绕x顺时针旋转,使得x的左子树成为x的父亲,同时修改相关节点的引用。旋转之后,二叉查找树的属性仍然满足
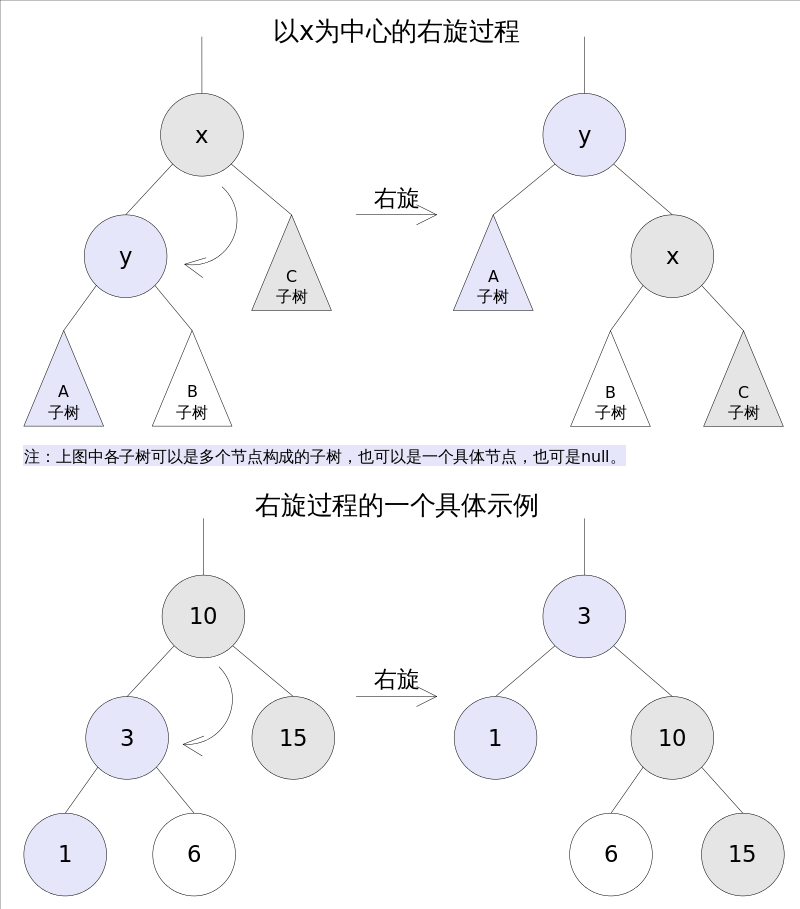
节点插入
首先需要先找到插入节点的父节点位置,与红黑树查找方式类似。以插入的节点为红色为例,当然也可以用黑色节点作为插入节点,但会更复杂。另外本文中所有节点中提到的值都指的是 Key,实际上节点还存在其它属性
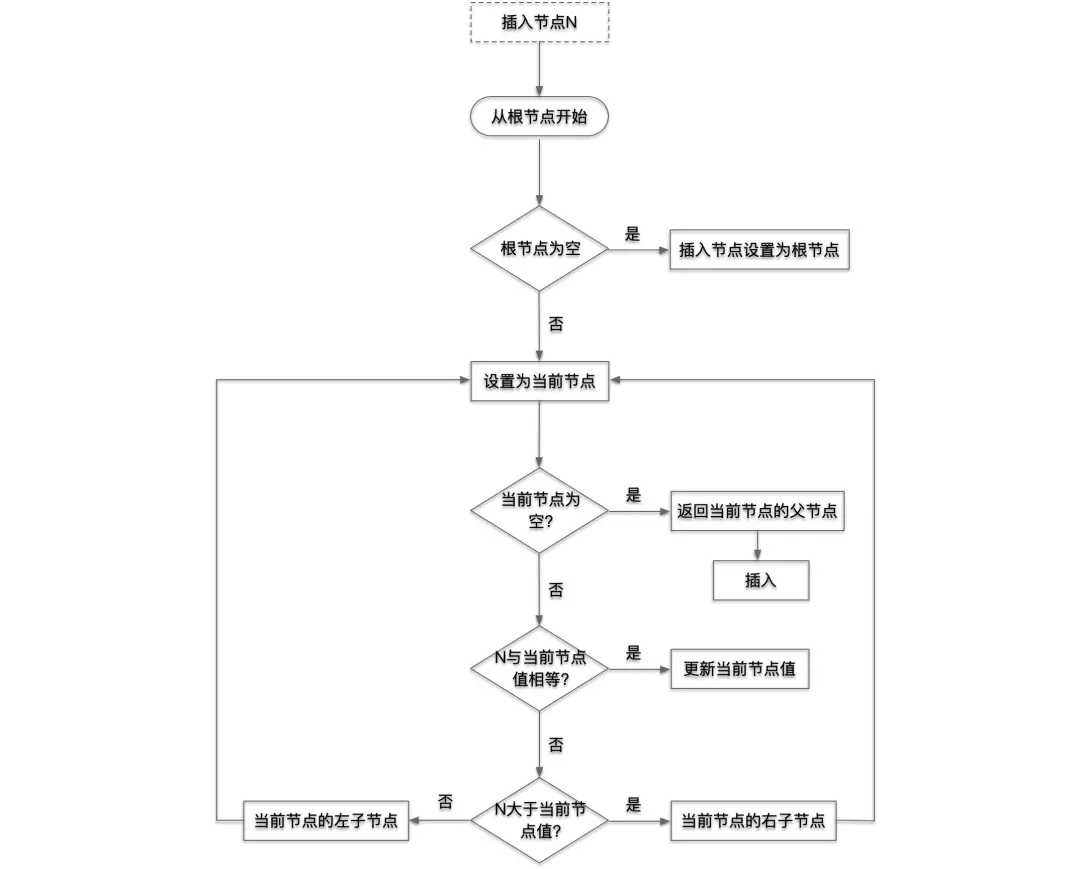
场景一:空树
根据红黑树性质第二点,红黑树根节点为黑色,即将插入节点修改成黑色即可;处理:插入节点 N 变成黑色节点并设置为根节点

场景二:插入节点 Key 已存在
在插入节点之前,红黑树是保持着平衡状态,只需要将插入节点的颜色变为被替换节点的颜色,同时替换掉原节点;处理:插入的节点 N2 变成原节点 N 的颜色并替换掉 N 节点;图中节点为灰色表示节点可以是红色或者是黑色

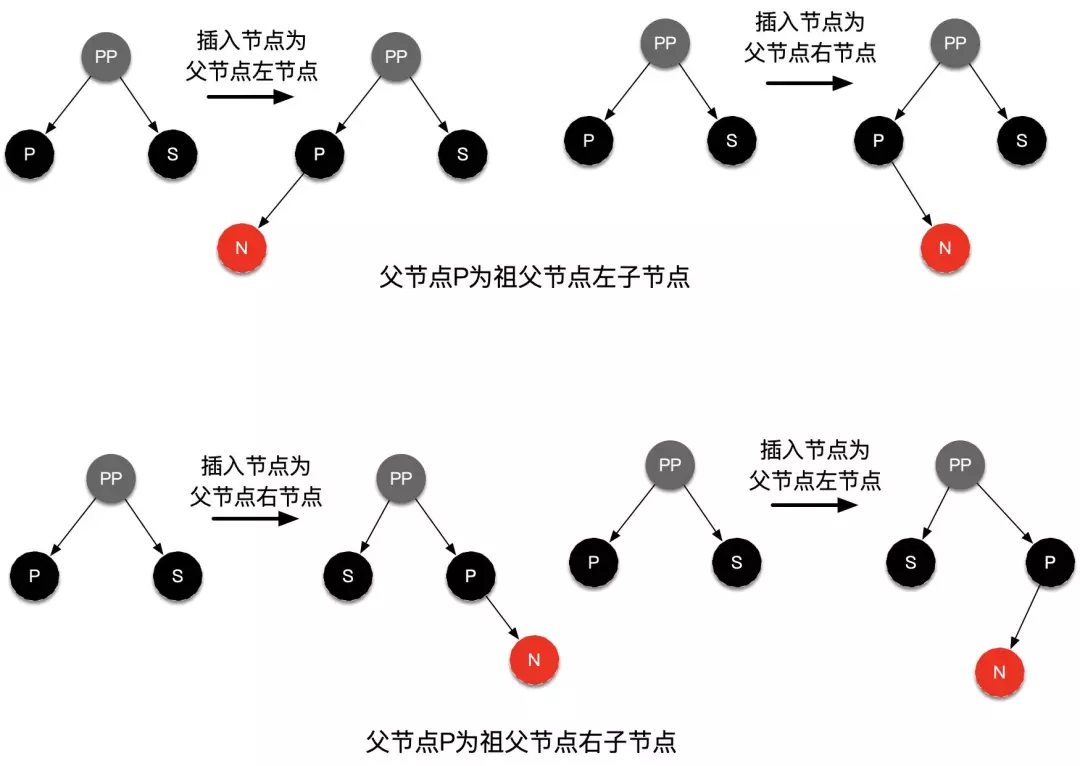
场景三:插入节点的父节点是黑色节点
插入的是红色节点 N,并不影响红黑树的平衡,插入之后不需要作其它处理
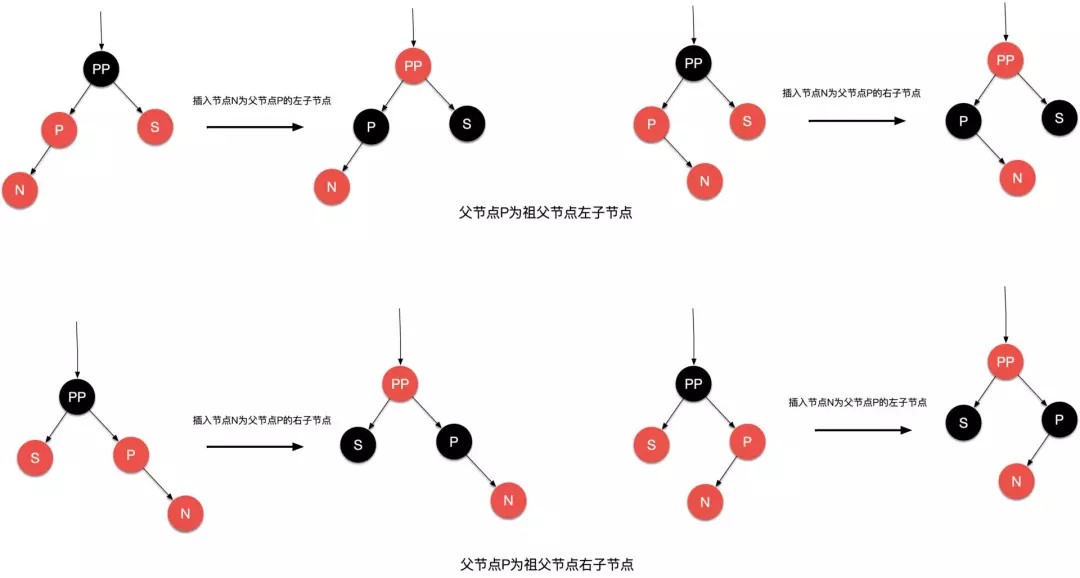
场景四:插入节点的父节点是红色节点且叔叔是红色节点
插入节点的叔叔节点是红色节点,根据红黑树性质 4 ,两个红色节点不能直接相连;处理:把父节点 P 及叔叔节点 S 由红色节点变成黑色节点,再把祖父节点 PP 变成红色,至此解决了插入节点与父节点两个红色节点直连的问题,并且黑色节点数量保持不变,但祖父节点由黑色变成了红色;如果祖父节点的父节点是红色节点应如何处理?处理:将祖父节点 PP 当作新插入的红色节点,从祖父节点的父节点开始由底向上进行处理,直至插入节点的父节点为黑色节点或者插入节点为根节点
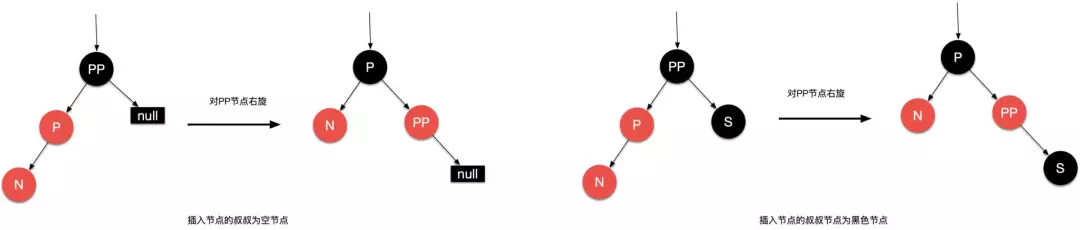
场景五:插入节点的父红点是红色节点,且叔叔节点是空 (null) 节点或者是黑色节点
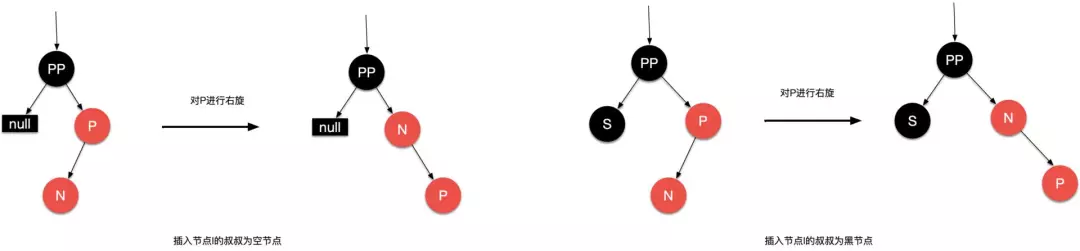
场景 5.1:插入节点 N 是父节点 P 的左节点且父节点 P 是祖父节点 PP 的左节点
叔叔节点是空节点这种场景好理解,下图中叔叔节点为黑色是什么情况,它不是已经处于非平衡状态了么?莫急,下图只是红黑树的局部图,回顾一下场景四由底向上处理时,祖父节点 PP 由黑色变成红色,对应到下图就是红色的父节点 P。处理:父节点 P 变成红黑色,祖父节点变成红色,并以祖父节点 PP 为支点进行右旋
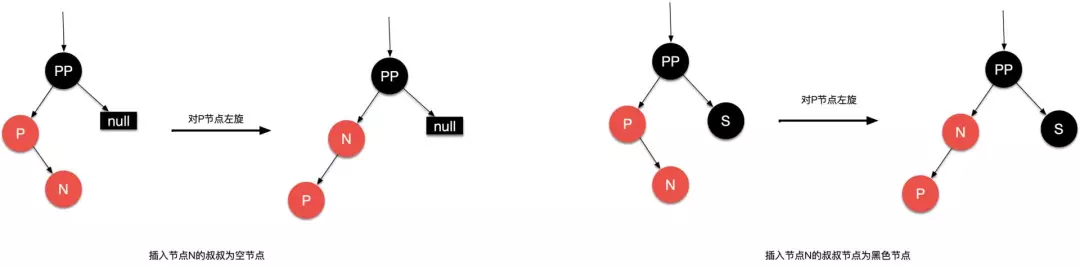
场景 5.2:插入节点是父节点的右节点且父节点 P 是祖父节点 PP 的左节点
处理:以插入节点的父节点 P 为支点进行左旋,转换到场景 5.1
场景 5.3:插入节点 N 是父节点 P 的右子节点且父节点 P 是祖父节点 PP 的右节点
处理:与场景 5.1 互为镜像,父节点 P 变成黑色,祖父节点变成红色,并以祖父节点 PP 为支点进行左旋
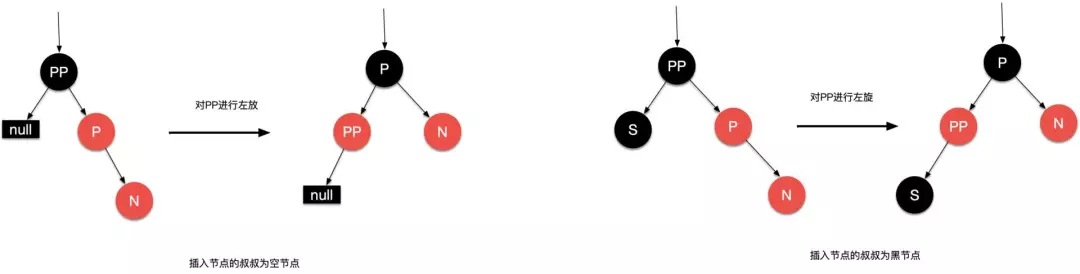
场景 5.4:插入节点的父节点的左子节点,父节点是祖父节点的右子节点
处理:与场景 5.2 互为镜像,以插入节点的父节点 P 为支点进行右旋,转换到场景 5.3